Origami Magic Crane and Graph Theory
Material: Square paper of any size that participants are comfortable with, pen/pencil, colored pencils, or crayons.
Objectives: Students understand the principle behind the two-colorable crane model and are introduced to graph theory, or be able to understand the proof to reinforce some concepts.
Topics: crease, flat foldable, graph concepts.
Activities:
- Instruct students on the steps involved in folding an origami crane, and encourage them to practice following each step.
Introduce students to fundamental concepts in origami, such as the traditional bases involved in constructing the crane, namely the Preliminary fold and the Bird Base (which can also be transformed into a Frog Base).
Explain key fold types such as the valley fold, mountain fold, and petal fold required to achieve the Bird Base, as well as the reverse fold used for shaping the crane’s head. To simplify the process, omit the step immediately prior to folding the crane’s head, as it introduces complexity to the crease pattern.
- Instruct them to reverse the steps and unfold the object, then use a pen/pencil to carefully trace the creases they made. Emphasize that the completed crane is a flat foldable origami model and explain the concept “flat-foldable model”.
- A model is considered flat-foldable if it can be compressed to a 2D shape without damaging any details. The shape that students have traced is known as a crease pattern, which serves as a blueprint for folding the origami model. Designing this crease pattern is crucial for constructing complex origami models. For more information on this, please refer to the origami article available on our website:
- https://wheremathmeetsart.com/en/2023/06/27/origami-how-numbers-revolutionized-an-art-form/
- https://wheremathmeetsart.com/vi/2023/06/30/origami-cach-nhung-con-so-cach-mang-hoa-mot-loai-hinh-nghe-thuat/
- The marked lines should resemble the image below, indicating whether each crease is a mountain or valley fold.
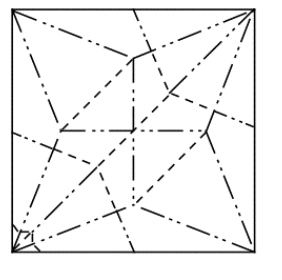
3. Present the problem: Consider the traced creases on one side of the paper. The goal is to color each area using only one color, ensuring that neighboring areas have different colors. The question is: What is the minimum number of colors needed for this task? The answer is 2.
4. Instructions for practice:
- Begin by coloring the crease pattern according to the given restrictions.
- Instruct the students to fold the paper back into the shape of a crane, using the crease pattern they have created.
- Observe the final outcome.
- Remember that all the colored regions should face one side, while the uncolored regions should face the other.
- As a slick proof for origami, each fold should separate the two adjacent areas into two regions facing opposite side.
- 5. Present a concise “origami proof” and rationale for converting this problem into a graph problem. Due to the complexity of explaining the terms involved thoroughly, the graph proof, if included, should only be a preliminary outline.
- Introduce the ideas of graph theory:
- Let’s first understand that it deals with the study of connections between objects, represented as nodes and edges. In simpler terms, graph theory is about exploring the relationships between these nodes. This field of mathematics is extremely versatile and can be applied to seemingly unrelated problems, such as social media friend lists, Sudoku puzzles, railway lines, plane routes connecting airports, and even geographical boundaries between countries on the map.
- Rigorous proof:
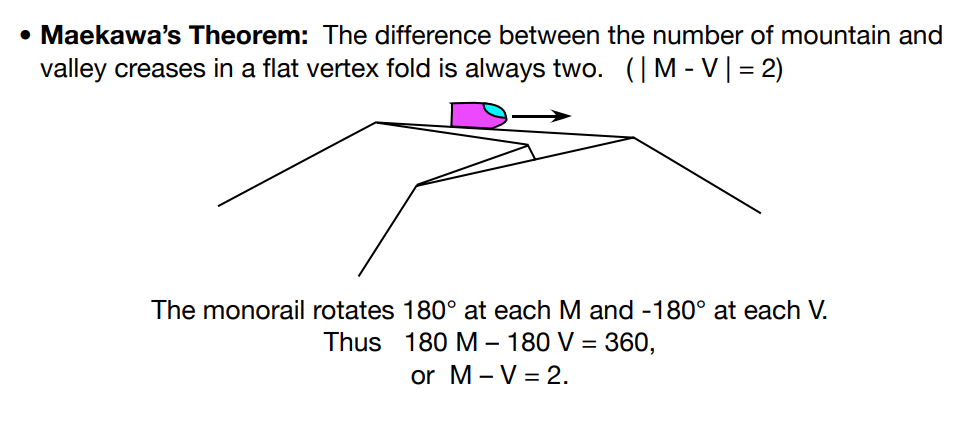
- To begin, we will establish that every vertex in the crease pattern has an even degree. This can be deduced from Makaewa’s Theorem, which states that the difference between the number of mountain creases (M) and valley creases (V) in a flat vertex fold is always equal to 2: |M-V| = 2.
- Proof: For a visual reference, please consult the accompanying figures.
Then consider the crease pattern, including the boundary of the square, as a planar graph. Along our line of argument, only the vertices on the boundary can have odd degrees. Connect all these vertices to a new vertice v. Since the number of odd vertices on a graph is even, v must have an even degree. (else it is the only vertice with an odd degree in this extended graph). The duals of planar graphs consisting of even-degree vertices only are bipartite. Therefore the dual is 2-vertex-colorable, meaning that our initial crease pattern and v is 2-face-colorable. We get the desired coloring by removing v.
