Origami: How numbers revolutionized an art form

Author: Tri Le

As early as the invention of paper, humans have been toying around with folding paper into aesthetically pleasing figures. Origami is an art form so easily accessible that children can pick up a square piece of paper and make a crane or two, yet artists are still breaking new ground in it today. So much has been done that they got from this:

to this

If you tried following diagrams in an origami book step-by-step, you would be like me and wonder: How did they pull it off?

The answer: with Math.

Overview and History

The word origami is simply the Japanese words for “folding” (ori) and “paper” (kami), combined in a single word used to describe the craft—and sometimes, art—of decorative paper folding. As the etymology suggests, this is the craft of transforming pieces of paper into certain shapes mainly by folding. In general, these designs begin with a square sheet of paper whose sides may be of different colors, prints, or patterns. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word kirigami to refer to designs that use cuts.

As stated before, paper-folding appeared in virtually all cultures paper could find its way to, namely Japan, Europe, and China, where the locals most likely developed their craft independently from other cultures up until the 20th century. In the beginning, that is when Buddhist monks brought paper to Japan in the 6th century, paper was still a precious commodity, so origami was only present on special occasions, and designs were simple and stylized, often depicting animals, costumed people, and ceremonial signs. The designs were passed down from mother to daughter. It’s reasonable to think that some complex designs were lost with time; nevertheless, the simple remaining ones still possess an enduring beauty. As paper gradually got easier to obtain, origami started to diverge from its “origata” (ceremonial origami) origin and signs of recreational origami started to appear at the end of the 16th century. Contrary to popular belief, traditional origami has often been less strict about modern conventions (which most likely sprang from the West), employing cuts more regularly. 

Moving on to the early 20th century, several artists, most notably Kosho Uchiyama and Akira Yoshizawa, the grandmaster of origami, started producing original designs. Yoshizawa in particular is praised to have raised origami from a craft to a living art, with at least 50 000 designs according to his own approximation, as well as introducing new folding techniques like wet folding – using water to slightly dampen the paper before a fold to give his figures more rounded and sculpted looks. Another brilliant innovation he made is the Yoshizawa-Randlett diagramming system for illustrating folding steps, which, after minor alterations by western authors Harbin and Randlett, standardized how origami instructions are written in books until this day. 

Let’s stop for a moment and think about the direction this art form will take from this point on. What happened in the 20th century? Countries becoming more and more interconnected, a technological boom, and the birth and dizzying development of computers, to name a few. Westerners were bound to flock to this art form, but what would they do with it? Can an artist, no matter how skilled, churn out designs if they had no particular method and just doodled with piece after piece of paper until the sheet was torn by the creases? 

Like any other type of art, there were patterns, motifs, and underlying principles behind origami. And like every real-world, tangible problem you want to know in-depth, Math can help you out. And indeed it did. 

The 1960s saw a flurry of activity in the Western folding world, with the establishment of two origami societies: the Friends of the Origami Center of America and the British Origami Society, both of which welcomed members from all over the world. The flat, two-dimensional origami was joined by modular origami, where similar units are assembled to form 3D, multi-faceted shapes. There was also a renewed interest in action figures, models that move when tugged. Pureland origami, created in the 70s to aid the learning process of beginners with limited motor abilities, restricts the folds one can make to mountain and valley folds. Not only did this constraint not hinder development, but it also helped artists to come up with minimalistically elegant designs. Since the 2000s, a new marriage of fields was on the horizon: origami tessellation. In origami tessellations, pleats are used to connect molecules such as twist folds together in a repeating fashion. Chris Palmer is an artist who has extensively explored tessellations after seeing the Zilij patterns in the Alhambra, and has found ways to create detailed origami tessellations out of silk. Robert Lang and Alex Bateman are two designers who use computer programs to create origami tessellations. The computational facet and the interchanges through social networks, where new techniques and designs are introduced, have raised the profile of origami in the 21st century.

Inside the creative process

Before we move on, some terms need to be brought up here for convenience

When we fold a piece of paper, the marks caused by the folds are called creases. The patterns of the folds on the paper that you get after undoing a model back to the initial stage of the folding process are called the model’s crease pattern. In broad strokes, there are three stages in the folding process: the piece of paper you use, the base you create, and the final model. It is important for you to remember, to understand, that a base is always the middle step. A base represents the foundation of all origami models. That’s why the most important step is picking the right base that has the same number of flaps (pieces of folded paper sticking out of the base) as the model you are trying to fold.  There are only a few traditional folds with minor tweaks and variations that come in handy:

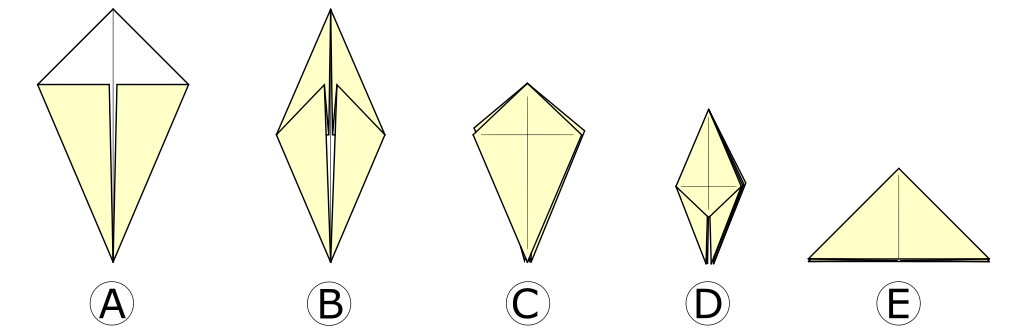
Depending on the model and the looks of the details you want to create, there will be different folding techniques, some of which may even be unique to a model (if you’re working on something elaborate enough). The picture below details some common folds you will want to know when you try out Origami:

Since the base is the most crucial part and the details can be filled in later on, the most important task at hand when you have something you want to represent by origami is finding a suitable base for it. By this time you may have realized that the traditional bases are inadequate, and doodling may take a lot of time in the dark. We need a method to construct that base.

Putting that problem aside, another great question arises: what designs are possible and what aren’t? Of course, that is too broad a question and usually artists are concerned with more specific versions of it. For example, you may ask the question: what does it take for a crease pattern to be flat-foldable (meaning that it can be folded into a 2D model)?

Let’s take a more scientific and mathematical look at an origami model. When you undo a model back to its initial stage, you get a crease pattern. Conversely, with a crease pattern, we can infer where the folds are and the type of the fold (mountain or valley), and a person who’s got no experience with the model can use the pattern and construct the base, completing the most important bridge to our end goal. With that in mind, how can artists make out such crease patterns for a base? 

One of the pioneers of modern maths-based origami, who certainly had no reservations about implementing technology into an art field,  is Robert J. Lang, an American mathematician and origami artist. In 1989, Lang wrote an article for the magazine Engineering & Science, in which he asked whether a computer could someday design an origami model deemed superior to those designed by humans. It was a question so intriguing that in 1990 he set out to write a computer program that could do just that.

Within several months, Lang had produced the first version of a piece of software he called TreeMaker (thus called because the figures he used as starting points resembled trees). It aids in a method called “circle packing”, which will be described below.

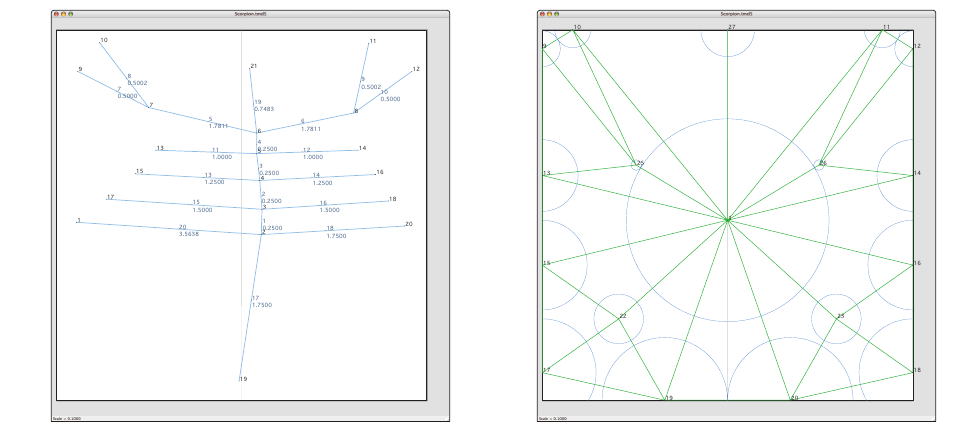
When you want to represent something using paper and folding, first select the main appendages and features of the thing you want to appear in the model. Then draw its “skeleton” using sticks and nodes only, noting that the lengths of the sticks are proportional to the size of the flaps. Here’s an example from Lang himself, taken from here, depicting the process of building a scorpion model:

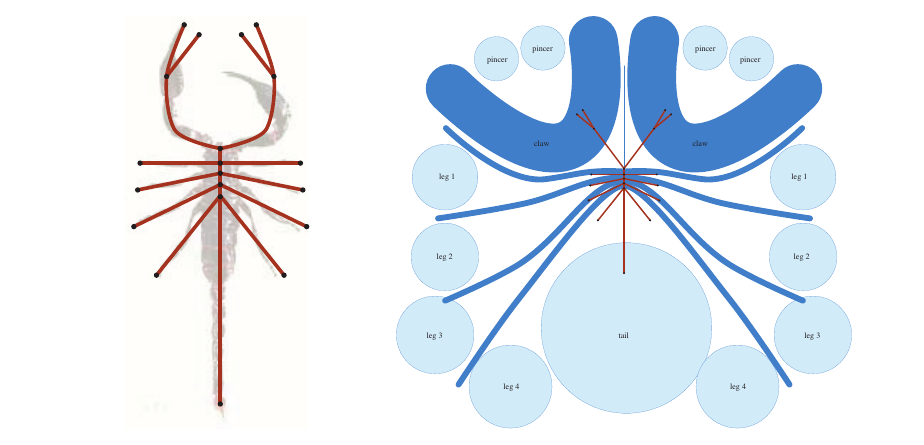
We then transform the stick figure into geometric shapes that represent regions of the paper required by each flap. These shapes are the light and dark regions in the figure. Flaps that are loose at one end, like the legs or pincers, are represented by circles (light), whose radius is equal to the length of the flap. Flaps that are connected to other flaps at both ends, like the body segments or the “arms,” are represented by constant width curves called “rivers” (dark); the width of the river is equal to the length of the corresponding flap. Each geometric shape—circle or river—represents the minimum amount of paper required for each of the flaps. It is a remarkable fact that for any valid arrangement of circles and rivers that specify the minimum paper needed, there exists a crease pattern that works for that exact arrangement of circles and rivers. 

And so, we must find the most tightly packed arrangement of the circles and rivers within a square. The major rules that apply to this packing are: 

• the circles and rivers must be as large as possible but maintain their same relative size to one another;

 • they may not overlap;

 • the circles do not have to be wholly inside the square, but their centers must be within the square; 

• the incidences between the various circles and rivers must match the incidences of their corresponding edges in the stick and node figure we made earlier

In many cases, Treemaker can quickly provide a solution for this optimization problem, and carry out the next step: figuring out the crease pattern to reach an appropriate base. The program will return the output in a fraction of a second since this is just a polynomial-time algorithm. Then, we fold and fill in the details.

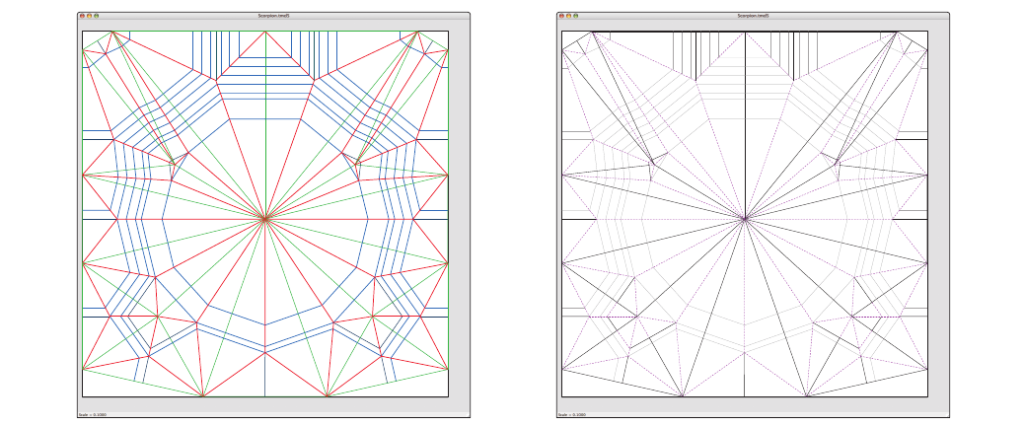
This doesn’t mean that it’s completely smooth sailing for an origami artist from this point on. The algorithm cannot fully control the width of the flaps, the cross-section, or the arrangement of layers. But this invaluable assistance is enough for a skilled artist, and the remaining steps, according to Lang, are easy.

The relationship between origami and math is not one-sided, however: Mathematical and computational origami are also attention-attracting fields. Thanks to the constant effort of mathematicians, there are certain restrictions we now know about flat-foldable models.

The construction of origami models is sometimes shown as crease patterns. The major question about such crease patterns is whether a given crease pattern can be folded to a flat model, and if so, how to fold them; this is an NP-complete problem. There are three mathematical rules for producing flat-foldable origami crease patterns:

1. Maekawa’s theorem: at any vertex, the number of valley and mountain folds always differ by two.
   It follows from this that every vertex has an even number of creases, and therefore also the regions between the creases can be colored with two colors.
2. Kawasaki’s theorem or Kawasaki-Justin theorem: at any vertex, the sum of all the odd angles adds up to 180 degrees, as do the even.
3. A sheet can never penetrate a fold.

Even at first glance, the connection between origami and Euclidean geometry is already clear. That’s why some classical geometry problems have been studied under the lens of origami, the most well-known of which to the public must be the Three construction problems of Antiquity. Two of which (doubling the cube and trisecting an angle) were shown to be feasible if we accept the constructions listed in the Huzita–Justin axioms that origami allows:

1. Given two distinct points p₁ and p₂, there is a unique fold that passes through both of them.
2. Given two distinct points p₁ and p₂, there is a unique fold that places p₁ onto p₂.
3. Given two lines l₁ and l₂, there is a fold that places l₁ onto l₂.
4. Given a point p₁ and a line l₁, there is a unique fold perpendicular to l₁ that passes through point p₁.
5. Given two points p₁ and p₂ and a line l₁, there is a fold that places p₁ onto l₁ and passes through p₂.
6. Given two points p₁ and p₂ and two lines l₁ and l₂, there is a fold that places p₁ onto l₁ and p₂ onto l₂.
7. Given one point p and two lines l₁ and l₂, there is a fold that places p onto l₁ and is perpendicular to l₂.

On a side note, if we turn each region bounded by creases in a crease pattern into a node, and the creases between those regions into edges, crease patterns can be studied as a graph theory problem. Other than the potential for mathematical research, these aspects of origami are also fruitful for lively Math classes in themes ranging from geometry to combinatorics and even topology.