Tessellation: Art in Recreational Mathematics and Maths Education
Author: Lê Vũ Minh Trí
In spite of our widely different conceptions of “beauty”, some motifs are universally regarded as “aesthetic”, such as symmetry, periodicity, and repeating patterns. Tessellation is an art form based on such elements, with an irresistible appeal not only to artists but also to mathematicians and curious students. We’ll focus on explaining the concept and its impact to the general public.
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps or gaps. The most notable example is the floor of your house or some yards.

As indicated by its deep history, one need not know any abstract geometry to create visually stunning tessellations. The earliest signs of tilings trace back to Sumerian houses and temples in 4000 BC, and a handful of other ancient civilizations took advantage of this art form, such as the Egyptians, Persians, Romans, Greeks, Byzantines, Arabs, Japanese, to the Chinese. In Medieval times, tessellation was exceptionally welcomed by Muslims and was featured extensively in their architecture. It would be a mistake were I not to mention the most prominent figure that revitalized this art form in the modern era, the Dutch graphic artist M.C. Escher and his intricate, mathematically inspired patterns. These days, we can find tessellation in a variety of architectural wonders from antiquity to modern days, textiles, quilting, and even cake decorating.

The author making a tessellation by modelling chocolate to decorate a cake

In Recreational Mathematics
Many games heavily employ elements of tessellation, ranging from jigsaw puzzles of thousands of pieces in size (each piece can be considered a tile with an image printed on), to practically any game with a square grid, such as sudoku, tic-tac-toe, and chess.
Polyominoes, an “invention” in the 1950s, is also a rich source of inspiration for Math games. A polyomino is a shape created by attaching same-sized squares in an edge-to-edge fashion. The most notable examples are polyominos made of 2, 3, and 4 squares, called dominos, trominos, and tetrominoes, respectively. Do they look familiar?
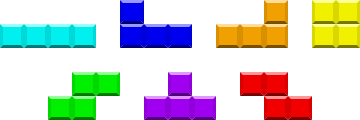
That’s right, the five types of tetrominoes and two flipped versions are the basis of Alexey Pajitnov’s familiar, simple yet addictive game Tetris. (now you know where the name comes from)
By replacing the square with other regular polygons, we can form some appealing variations, such as the polyhex composed of regular hexagons, and the polyiamonds made of equilateral triangles.
In recent years, there has been a trend of bridging tessellation and another well-established art form, Origami, pioneered by Alessandro Beber, Robert Lang, Ekaterina Lukasheva, and Chris Palmer. To create the effect of tessellation on paper, they first form a dense crease pattern, then fold where needed to create regular or stellated polygons, etc, resulting in mesmerizing works.
Another topic of interest is the hinged dissections of Henry Dudeney, dissections of a shape into pieces connected by hinges to form a chain.
In Mathematics Education
It’s no challenge finding a satisfying tessellation pattern, the appeal of this art form to kids is even greater than to adults. Therefore, tessellation has been taught by educators all across the globe. It is rarely, if ever, listed as compulsory in public education though, despite its ability to lively demonstrate many elements of geometry. Such elements include basic recognition of symmetry, geometrical transformations (rotation, translation, reflection), congruence of two shapes, and computational theorems such as Pythagoras’ theorem. As for those having some experience with Olympiad-oriented Maths, you may find some topics of Combinatorics and coloring techniques feature problems with a square grid or polyominoes.
To wrap up, here are some ideas for lessons with tessellation:
Activity 1: Recognizing tessellations
Materials: Copies of Worksheet 1.1
Objective: Learn to tell if a collection of shapes is a tessellation or not
Vocabulary: Tessellation, infinite, mathematical plane
Activity Sequence
- Write the definition of a tessellation on the board. Be sure the class understands it and also what the terms infinite and mathematical plane mean.
- Pass out copies of the worksheet.
- Have students circle those patterns that are tessellations and put an “X” through those that aren’t
Discussion Questions
- Is pattern letter a/b/c/d/e/f a tessellation?
- Why or why not?
- If it isn’t, how might it be changed to make it into a tessellation?

Activity 2: Basic properties of tiles
Materials: Copies of Worksheet 2.1
Objective: Learn to identify tiles and their edges and corners
Vocabulary: Tile, polygonal space, edge, corner
Activity Sequence:
- Write the vocabulary terms on the board and discuss the meaning of each one
- Pass out copies of the worksheet
- For each shape, have the students circle those that are tiles and X through those that aren’t
- For the polygonal tiles, have the students put a C by each corner and an E by each edge
Discussion Questions:
- Is the shape a/b/c/d/e/f/g/h a tile or not?
- Why or why not?

(Source of lessons: Robert Fathauer – Tessellations: Mathematics, Art, and Recreation-CRC Press (2021) )
