Tessellation: Nghệ thuật trong Toán thường thức và việc dạy Toán

Tác giả: Lê Vũ Minh Trí

Quan niệm về cái đẹp của mỗi người là mỗi khác, nhưng vẫn tồn tại những motif có thể được đại đa số coi là “thẩm mỹ”, chẳng hạn như tính đối xứng, sự tuần hoàn và họa tiết lặp lại. Tessellation là một loại hình nghệ thuật dựa trên những tiêu chí ấy, mang trong mình sức hấp dẫn mạnh mẽ không chỉ với giới nghệ thuật mà còn với cả các nhà toán học muốn đào sâu nghiên cứu và cả những học sinh hiếu kỳ. Phần này chúng ta sẽ tập trung vào giải nghĩa khái niệm này và nêu lên tác động của loại hình này với đại chúng.

Tessellation, tiling hay lát gạch là một cách phủ toàn bộ bề mặt nào đó, thường là mặt phẳng, bằng một hoặc một vài hình khối, gọi là ô gạch (tile), sao cho không có hai hình nào chồng lên nhau hay để lại khoảng trống. Ví dụ đơn giản nhất có thể kể đến chính là sàn nhà và sân của bạn.

Chẳng cần phải biết tường tận về hình học để sáng tạo ra những mẫu tessellation thỏa mãn thị giác, như được chỉ ra bởi lịch sử lâu đời của môn nghệ thuật này.Dấu tích sớm nhất của lát gạch xuất hiện vào những năm 4000 TCN trong nhà và đền thờ người Sumer, và không ít nền văn minh cổ đại đã tận dụng loại hình nghệ thuật này, từ Ai Cập, Ba Tư, La Mã và Hy Lạp, Byzantine, Ả Rập, Nhật Bản, cho tới Trung Quốc. Đến tận thời kỳ Trung cổ, tessellation được người Hồi giáo ưa chuộng và là một phần nổi bật trong nghệ thuật và kiến trúc của họ. Tới thời hiện đại, không thể không kể đến những sáng tạo có sức ảnh hưởng lớn của M.C.Escher, một nghệ sĩ đồ họa người Hà Lan với những tác phẩm tessellation đậm chất Toán học và không kém phần ảo diệu, đê mê. Ngày nay, ta vẫn có thể bắt gặp các hoạt tiết tessellation trong các kiến trúc từ cổ điển đến hiện đại (đặc biệt là sàn nhà), các sản phẩm dệt may, chăn gối, các loại hình nghệ thuật như hội họa, thậm chí là trang trí bánh, v.v.  

Tác giả đang lát một mẫu tessellation bằng modelling chocolate để trang trí bánh

Trong Toán thường thức

Chiếu theo định nghĩa trên, tessellation bao hàm rất nhiều trò chơi quen thuộc, từ những bộ xếp hình lên đến hàng nghìn miếng: mỗi miếng có thể coi như một ô gạch được in một phần hình ảnh lên, cho tới kha khá trò chơi chứa lưới ô vuông như sudoku, cờ vua, hay cờ caro. 

Polyomino, một “phát minh” từ những năm 50 thế kỷ trước, là nguồn cảm hứng dồi dào cho lĩnh vực này. Một polyomino là một hình được tạo ra bằng cách nối khít các cạnh của những hình vuông cùng cỡ với nhau. Tiêu biểu nhất là các polyomino tạo từ 2, 3 và 4 hình vuông cùng cỡ, gọi là domino, tromino và tetromino.

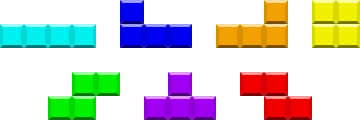
Đúng rồi đấy, dựa vào 5 loại tetromino cộng thêm hai ô đối xứng, kỹ sư máy tính người Nga Alexey Pajitnov đã sáng tạo nên trò chơi Tetris đơn giản mà gây nghiện với không ít người. 

Ta có thể tạo ra những biến thể từ việc thay thế hình vuông bởi các đa giác đều khác, ví dụ như polyhex cấu tạo từ các lục giác đều và polyiamonds từ các tam giác đều. 

Những năm gần đây, một trào lưu mới đang dần kết nối môn nghệ thuật này với một lĩnh vực liên kết chặt chẽ không kém với Toán – Origami. Những người tiên phong có thể kể đến Alessandro Beber, Robert Lang, Ekaterina Lukasheva, và Chris Palmer. Để tạo nên hiệu ứng tessellation trên tờ giấy, họ sẽ tạo ra những mạng nếp gấp dày đặc và gập tại một số nơi, cho ra những đa giác đều, hình ngôi sao, v.v. 

Một chủ đề thú vị khác là hinged dissection (tạm dịch là phân chia khớp nối) của Henry Dudeney, một cách cắt một hình ra làm các mảnh được các “khớp” nối liền thành một dải.

Trong việc giảng dạy Toán

Không khó để ta tìm thấy một hoặc một số mẫu tessellation nào đó “đẹp”, điều này hấp dẫn  những đứa trẻ ở độ tuổi đi học còn mạnh mẽ hơn với người lớn nữa. Do vậy, bộ môn lát gạch đã được nhiều giáo viên khắp nơi sử dụng trong quá trình giảng dạy. Ở Việt Nam nói riêng và hầu hết các quốc gia khác nói chung, đây là một nội dung không bắt buộc trong chương trình, thế nhưng tessellation có thể minh họa khá sinh động nhiều kiến thức hình học. Các kiến thức này đến từ mức độ nhận biết cơ bản về sự đối xứng, cho tới các phép biến hình (quay, đối xứng trục, tịnh tiến), sự bằng nhau của hai hình và các định lý tính toán như định lý Pytago. Với những ai đã có trải nghiệm với Toán chuyên, các chuyên đề Tổ hợp và Tô màu có không ít bài toán có sự góp mặt của những miếng polyomino và lưới ô vuông. 

Để kết lại, sau đây là một số ý tưởng bài giảng về tessellation:

Hoạt động 1: Nhận biết Tessellation

Học liệu: Phiếu 1.1

Mục tiêu: Phân biệt một tập hợp các hình có phải tessellation không

Khái niệm: Tessellation, vô hạn, mặt phẳng Toán học

Các hoạt động

1. Viết định nghĩa của tessellation lên bảng. Đảm bảo học sinh hiểu khái niệm này và “vô hạn”, “mặt phẳng Toán học” là gì.
2. Phát phiếu trên
3. Học sinh khoanh tròn các họa tiết là tessellation và gạch chéo các họa tiết không phải tessellation

Câu hỏi thảo luận

1. Các hoạt tiết từ a đến f có phải tessellation không?
2. Tại sao (không)?
3. Nếu không thì thay đổi thế nào để thành tessellation?

Hoạt động 2: Các tính chất cơ bản của ô gạch (tile)

Học liệu: Phiếu 2.1

Mục tiêu: Nhận biết được thế nào là ô gạch, góc và cạnh của chúng

Khái niệm: Ô gạch, gạch đa giác, cạnh, góc

Các hoạt động

1. Viết các khái niệm lên bảng và giải nghĩa chúng
2. Phát phiếu 2.1
3. Học sinh khoanh tròn những hình là ô gạch và gạch chéo những hình không thỏa mãn định nghĩa
4. Với các ô gạch đa giác, học sinh đánh dấu G để chỉ góc và C để chỉ cạnh

Câu hỏi thảo luận

1. Các hình từ a đến h có phải ô gạch không?
2. Tại sao (không)?

(Nguồn bài giảng: Robert Fathauer – Tessellations: Mathematics, Art, and Recreation-CRC Press (2021) )