PenRace and Creating Tessellations (Pt 2)

The slides and the quiz

An explanation for 5:

 The interior angles of an arbitrary n-gon add up to 180.(n-2), and so each angle of a regular n-gon is 180(n-2)/n. A vertex of an n-gon that can tile the plane by itself has to be surrounded by copies of such an n-gon. This means that a whole revolution, or 360 degrees, is a multiple of the interior angle of the n-gon. In other words, 

360/ (180(n-2)/n) = 2n/(n-2) is a whole number

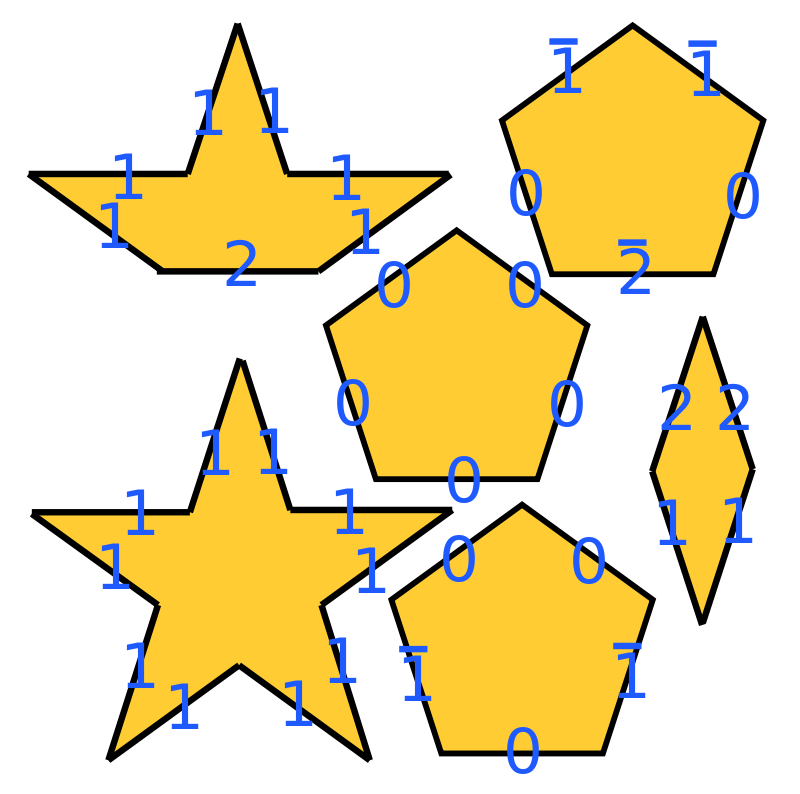
Since n>=3, the only values satisfying this are 3, 4, and 6. Indeed there are tessellations with equilateral triangles, squares, and hexagons. 5 is the smallest number that “fails” this test, so we can suspect that there is something not periodic about fivefold symmetry. 

A more simple and looser explanation:

Notice how two angles of a regular polygon of 7 sides or more is never a full 360-degree angle, but three exceeds 360 degrees. (visualize)

How to use Tiled.art: https://tiled.art/en/home/

1. Choose a type of tile & symmetry based on your intended purpose (types are based on the Wallpaper group I think)
2. Add points to the boundary of the tile to morph its shape. The mechanisms of the website ensure that changes are applied simultaneously in connected areas.
3. When you have finished building the shape of the tile, press the folder symbol to the left and save it as an Inkscape tile, .svg. Download Inkscape for better drawing tools for the tile. Upload and revert (ctrl+E) to show the results of the decorating tiles in action. 

Overview of Penrose Tiles: three types: 

• P1: 6 tiles, drew inspiration from Kepler, not optimal yet

• P2: Kites and darts

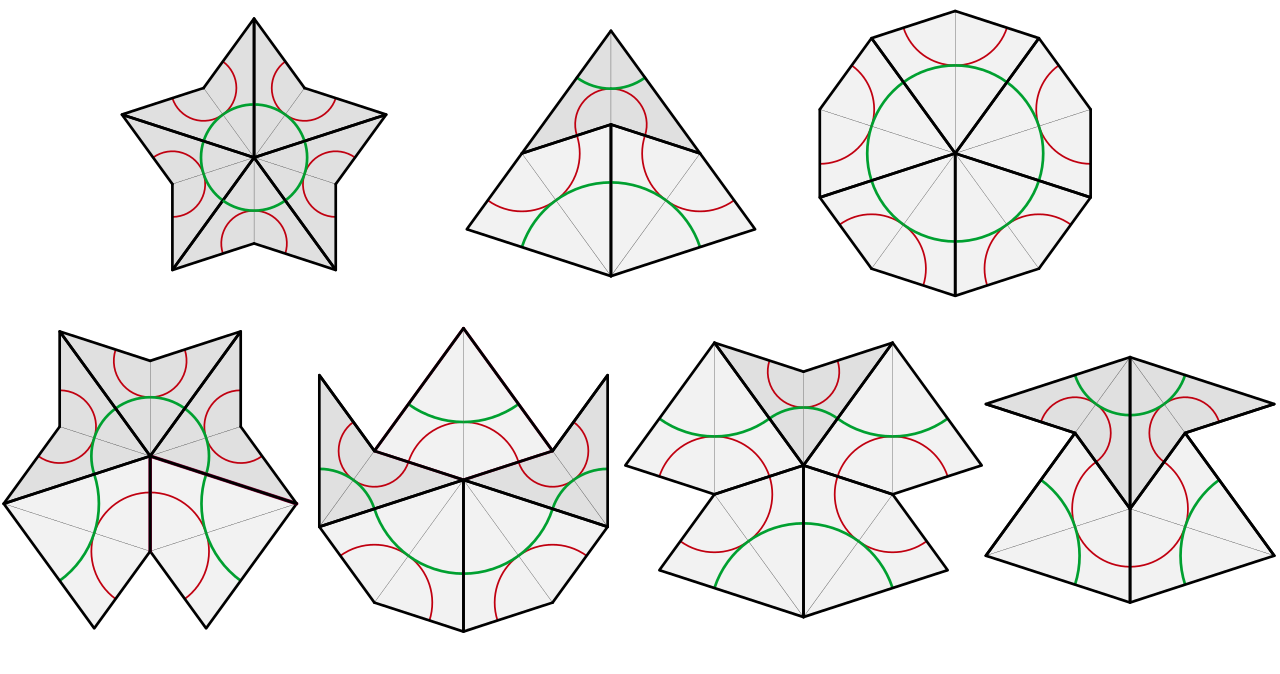
Kite and dart tiles (top) and the seven possible vertex figures in a P2 tiling, which are each given nicknames as follows – First row: star, ace, sun. Second row: king, jack, queen, deuce

The circular arcs are added to enforce the tiling rule, else we can just join them to make a full diamond/ rhombus and tile the rhombi edge-to-edge.

• P3: Rhombus tiling

Two ways to enforce an aperiodic tiling rule. The reasoning is similar to P2. 

The props for the game should either be P2 or P3, without details enforcing aperiodicity (just put that in the rules). The unenforced P3 structure gives rise to a pattern like this:

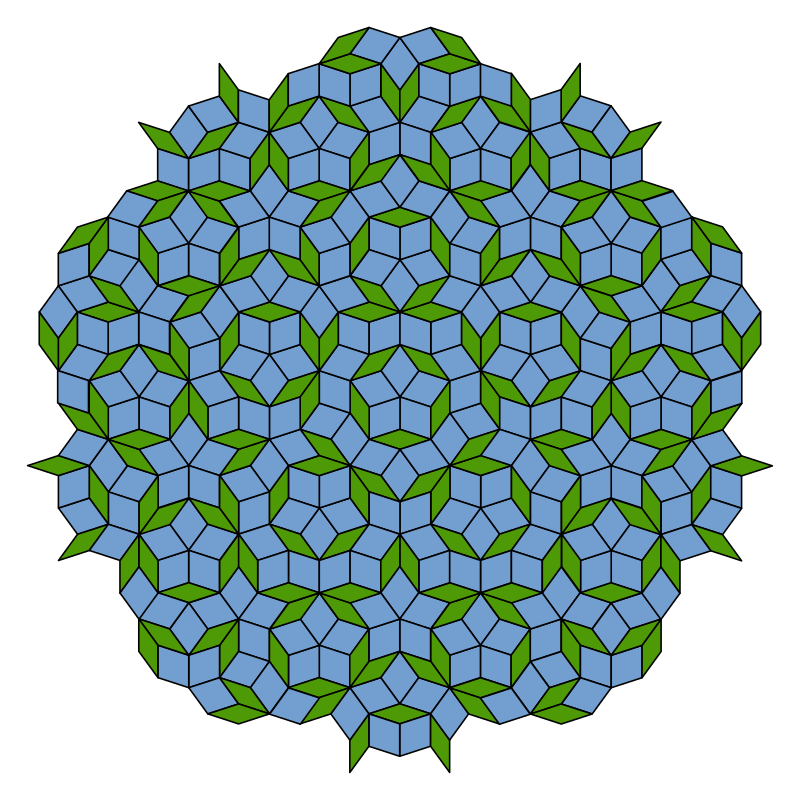
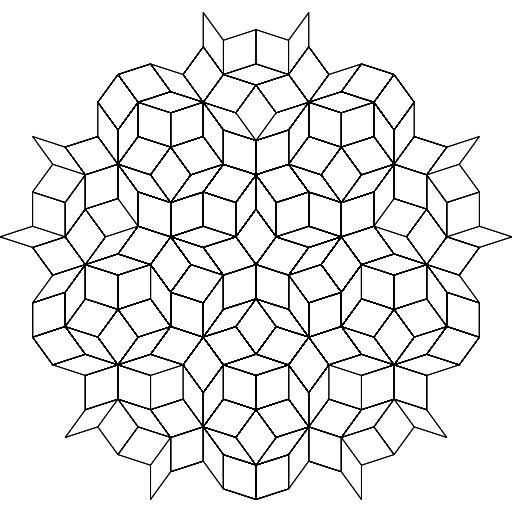
The blue rhombus has an angle of 72 while the green one has an angle of 36.

SCRIPT

What is a tessellation? It’s the covering of a surface, most often a plane, with shapes such that there are no gaps or overlaps (emphasize the no gaps or overlaps). We can find tessellations in many places in our daily lives, showing just how prevalent this type of decoration is, and how there is an innate pattern seeker, in other words, a geometer, in all of us.

(pavements, brick walls, mosaics, pottery, etc.)

(Typical tile) In simpler terms, a tile is a set whose boundary is a single simple closed curve. In this context, the term curve includes straight line segments, so basically any single two-dimensional shape without holes is a tile. Tiles also shouldn’t neck down to points or lines anywhere. The area inside the curve, or boundary, is the interior of the tile. A polygon is a closed figure on the plane made up of straight-line segments. For a polygonal tile, the individual segments are referred to as edges, and the points where two edges meet are referred to as corners.

Two of the most prevalent math themes at the heart of tessellations are symmetries and geometric transformations. With seventh-grade geometry, we can show that all transformations that preserve the shape and size of something are one of the four types: translation, rotation, reflection, and glide reflection. 

• Translation: you shift all the points of the shape the same way in the same direction
• Rotation: this is just how you usually think of rotation
• Reflection: turns a shape into its mirror image 
• Glide-reflection: a translation and reflection 

Of course, we can find symmetries in natural and everyday objects 

(leaves, rackets, moths, or most animals actually, sea stars, windows, tires, and flowers)

A tessellation is said to possess translational symmetry if the infinite tessellation can be translated, and remain unchanged (perfectly overlies itself). A tessellation that possesses

translational symmetry is said to be periodic. The translation vector for an infinite tessellation is not unique. A tessellation is said to possess n-fold rotational symmetry about a point (where n is an integer) if the entire tessellation can be rotated by 1/n of a full revolution about

that point and remain unchanged. The smallest rotation amount should be specified; i.e., if a tessellation possesses six-fold rotational symmetry, it also possesses three-fold and two-fold, but it is referred to as six-fold. A polygon can be used both to indicate a point

of rotational symmetry and to specify the amount of rotation. For example, a rectangle

is used to indicate a point of two-fold rotational symmetry, an equilateral triangle of three-fold, a square of four-fold, a hexagon of six-fold, and so on. A tessellation is said to possess glide-reflection symmetry if the entire tessellation can be translated along some line and then reflected about that line and remain unchanged. Mirror symmetry is a special

case of glide reflection symmetry, in which the glide distance is zero.

In a periodic tessellation, there are an infinite number of equally spaced lines of a

given type, unless the tessellation is only periodic in the direction parallel to the line

PROBLEM:

Polygons are familiar tiles, so let’s investigate some of their properties

• Which polygons can always tile the plane on its own?
• Which regular polygon can tile the plane in one size?

APERIODICITY 

As I’ve said before, a tessellation is called periodic if there is a (nonzero) translation in some direction that keeps the pattern unchanged. Anything set of tiles that can only tesselate in non-periodic ways is called “aperiodic”. An immediate question is “Do they exist? And at least how many types of tile are needed to tile aperiodically only? ”. The answer is yes, and the first set of tiles that may achieve that has 20426 tiles!

For a long time, some tiles have been proposed, but they unfortunately fail some criteria of the problem (such as the Socolar-Taylor tile), and mostly the consensus was that the best we have had been 2. Until very recently, just November last year, David Smith, a hobbyist, found the tile holding the answer. He called it “the hat”, and it along with its reflected version, can tile aperiodically. That discovery made headlines, but some argued that the reflected tile is a different tile, so this doesn’t bring the answer down to 1. But David was far from done with discovering the tile. As he was playing around with the Tile(1,1), one of the infinite variants in the hat’s family, he made a slight modification that settled the problem once and for all, since this tile no longer requires the reflected version.