Fractal: Ngôn ngữ của tự nhiên, nghệ thuật, và toán học

Dịch giả: Nguyễn Duy Anh

Hãy nghĩ đến một hình vuông, một hình chữ nhật, hay một hình tam giác đều. Giờ hãy nghĩ về một thứ gì đó “tự nhiên” – có nguồn gốc tự nhiên vớ sự can thiệpi tối thiểu bởi bàn tay con người. Bạn có nghĩ ra được thứ nào tự nhiên như vậy mà là một hình chữ nhật hoàn hảo, một góc 60 độ không lệch chút nào, hay thậm chí là một đường thẳng hoàn hảo không? Khả năng là không, Alan Watts, một triết gia nổi tiếng, cũng nghĩ vậy. Trích lời của ông, sử dụng ngôn ngữ của Đạo giáo, một nhánh triết học cổ Trung Quốc về “Đạo” – “con đường” của tự nhiên:

“Đạo là một kiểu trật tự nhất định, và nó không giống với cái ta gọi là trật tự khi ta sắp xếp mọi thứ theo quy tắc như là theo hàng hay theo cột. Nó là một kiểu trật tự thô, nhưng khi bạn nhìn vào một cây tre, rõ ràng là cây tre có một trật tự nào đó. Ta nhận ra ngay lập tức nó không hỗn độn, nhưng nó không đối xứng và nó không thuộc về hình học. Cái cây ấy nhìn trông như một bức họa Trung Quốc vậy. Người Trung Quốc yêu thích trật tự bất cân xứng này tới mức họ đưa nó vào trong tranh vẽ. Trong tiếng Trung nó được gọi là “li”, và hán tự của “li” ban đầu mang nghĩa là những dấu vân của ngọc bích. Nó cũng có nghĩa là các vân của gỗ và các thớ cơ. Ta cũng có thể nói, các đám mây có “li”, đá cẩm thạch có “li”, cơ thể con người cũng có “li”. Tất cả chúng ta đều nhận ra nó, và mọi nghệ sĩ, dù là họa sĩ phong cảnh, họa sĩ chân dung, họa sĩ trừu tượng, hay họa sĩ không khách quan, đều cố bắt chước nó. Họ đều đang cố thể hiện cái tinh hoa của “li”. Điều thú vị là dù ta đều biết nó là gì, không có cách nào để ta có thể định nghĩa nó.”

Alan W. Watts in Taoism: Way Beyond Seeking, The Edited Transcripts, ed. Mark Watts, Charles E. Tuttle Co., Boston, 1997.

Vào những năm đầu của thập niên 1970, điều này khá đúng. Watts qua đời năm 1973, và điều này nghĩa là ông đã bỏ lỡ một công trình đạt được chính xác điều mà ông cho là khó khăn: tìm ra thứ toán học mô tả hình học của tự nhiên. Tên của công trình đó là “Hình học fractal của tự nhiên” bởi không ai khác ngoài Benoit B. Mandelbrot (Người ta hay đùa rằng chữ B. trong tên ông là viết tắt của Benoit B. Mandelbrot)

Fractal, còn được gọi là hình phân dạng, có gốc tiếng La tinh là từ “fractus”, nghĩa là “bất quy tắc” hay “phân mảnh”. Khi nhắc đến fractal, người ta hay nghĩ đến những hình dạng có một phần là một phiên bản thu nhỏ của toàn thể. Nhưng đây là một sự đơn giản hóa quá mức, và rất khó để tìm được một định nghĩa tổng quát cho fractal. Hiện tại, ta sẽ sử dụng ý hiểu chung nói trên và xem một vài ví dụ để nắm được fractal thể hiện điều gì.

Các ví dụ kinh điển

Bắt đầu với một tam giác đều và chia nó làm 4 tam giác đều nhỏ hơn. Bỏ hình ở giữa đi và lặp lại cho 3 tam giác đều còn lại. Lặp đi lặp lại thao tác trên và thứ ta thu được được gọi là tam giác Sierpinski

Chia hình vuông thành 9 phần và bỏ đi hình vuông ở giữa, sau đó lặp lại thao tác đó với 8 hình vuông còn lại, ta sẽ có một thứ gọi là tấm thảm Sierpinski. Một fractal tương tự, được tạo nên bởi các đoạn thẳng thay vì các tam giác hay hình vuông, được gọi là một tập hợp Cantor: bắt đầu với một đoạn thẳng, chia ba nó, sao chép phần đầu và phần cuối rồi để xuống dưới, cách đoạn ban đầu một khoảng, và lặp lại với mỗi đoạn thẳng mới.

Dĩ nhiên, ta có thể tổng quát hóa một vài cấu trúc này. Ví dụ, ta có thể tạo ra một fractal với các khối hình ba chiều thay vì hai chiều, chẳng hạn dùng các hình tứ diện đều để tạo ra tứ diện Sierpinski, hay dùng các khối lập phương thay cho các hình vuông để thu được một bọt biển Menger.

Một fractal nổi tiếng khác là đường cong Von Koch có cách dựng như sau:

Từ đoạn thẳng khởi đầu, chia nó làm 3 đoạn bằng nhau, dựng một tam giác đều hướng lên trên với đoạn thẳng chính giữa rồi bỏ đoạn thẳng chính giữa đó đi. Lặp đi lặp lại thao tác đó với những đoạn thẳng thu được.

Thực hiện thao tác này với 3 đoạn thẳng của một tam giác đều và ta thu được một bông tuyết Von Koch.

Đến giờ, hẳn bạn đã nhận ra điểm chung của những fractal này: ta bắt đầu với một hình khởi điểm và một dãy các thay đổi hình học được thực hiện liên tục. Nói cách khác, ta thực hiện tương tự một hệ thống các hàm vô hạn lần. Đây cũng là lí do vì sao phương pháp dựng fractal này được gọi là “Iterated Function System” (hay IFS), dịch ra là “Hệ thống hàm lặp”. (Giờ thì các bạn hiểu vì sao cái câu đùa về Benoit B. Mandelbrot buồn cười rồi). Đây cũng là phương pháp các máy tính sử dụng để kết xuất những cấu trúc bất khả thi này.

Ngôn ngữ của tự nhiên dưới dạng toán học

Sự lồi lõm và phức tạp của một fractal ở mọi quy mô khiến chúng trở nên rất thích hợp để mô tả sự thô ráp của các vật thể tự nhiên mà hình học Euclid không thể thể hiện đầy đủ. Vì hiển nhiên con người không thể lặp lại một thao tác vô hạn lần, và các nguyên tử thì cũng không thể chia nhỏ vô hạn lần, ta chỉ cần thực hiện thao tác đủ nhiều lần khi cố gắng tạo ra hình ảnh các fractal. Ta sẽ có thể mô phỏng hiệu ứng của một fractal hoàn chỉnh vì các chi tiết nhỏ hơn là gần như không thể nhìn thấy được

Khi bạn đọc đang đọc phần này, bên cạnh người nếu có bút và giấy thì tốt, vì trăm nghe không bằng một thấy, và trăm thấy không bằng một làm. Sau đây là vài ví dụ

Súp lơ trắng: So sánh từng ngọn và toàn bộ bông

Súp lơ Romanesco: từng nhánh đều tự đồng dạng

Các dãy núi cũng có dạng fractal. Thật ra ảnh bìa của bài báo này được kết xuất do một thuật toán dùng fractal. Có ai tưởng đó là núi thật không?

Giờ ta thử vẽ một thứ bằng “tư duy của fractal” nào. Đầu tiên, dùng bút chì (đầu nên nhọn) để vẽ một cành cây không có lá, chẳng hạn:

Nhớ hình này, sau đó tẩy từng nhánh nhỏ đi và thay bằng cành bạn vẽ ban đầu ở tỉ lệ hợp lý, khi đó ta được một thứ kiểu như sau:

Chưa giống đến thế, nhưng nếu bạn đủ kiên nhẫn để làm tương tự vài lần nữa, thì hoặc đến một lúc đầu bút của bạn không đủ nhỏ, hoặc bạn được:  

Phương pháp này có thể áp dụng cho các loài thực vật khác, tùy vào hình dạng ban đầu bạn vẽ và chi tiết ta thay thế sau mỗi bước.

Đây là một danh sách chi tiết của những nơi fractal xuất hiện trong tự nhiên (nguồn khá rõ ràng):

Số chiều fractal: góc nhìn Toán học 

Dĩ nhiên, những fractal đã con mắt không nằm ngoài khả năng nghiên cứu có hệ thống của chúng ta. Phát triển từ hiểu biết sẵn có về hình học thông thường, ta bắt đầu bằng việc thử áp dụng những khái niệm đang tồn tại cho fractal, bắt đầu với chiều không gian. Như ta sắp thấy ở đây, ta phải làm lại khái niệm này theo một cách hơi không chính thống.

Vào năm 1921, nhà toán học người Anh Lewis Fry Richardson, trong một trong những khoảnh khắc kì lạ khi ông cố áp dụng toán học vào những chủ đề khác thường, thử động chạm đến vấn đề đo độ dà đườngi bờ biển. 

Ý tưởng của Richardson là chọn một “độ dài bước đi” s rồi tính xem phải đi bao nhiêu bước thì mới đi hết đường bờ biển. Ví dụ, xét một lần đi từ Land’s End đến Duncansby Head, điểm khởi đầu và điểm kết thúc Richardson chọn. Với s = 100km, ta phải đi 28 bước, vậy Richardson ước tính độ dài của đường bờ biển là 28 s. Ta xem trong hình đầu tiên:

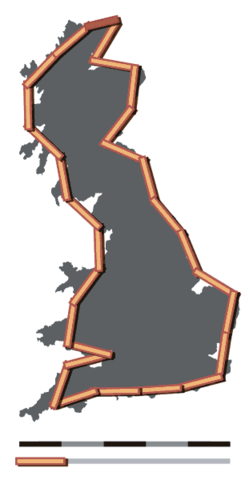
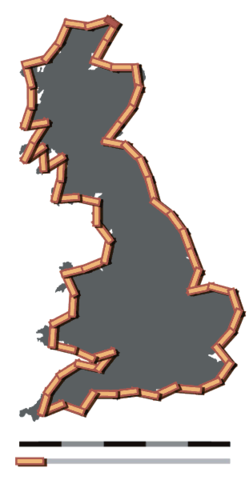
Tuy nhiên, ta thấy một độ dài bước đi lớn như vậy sẽ bỏ qua rất nhiều chi tiết của đường bờ biển – những chỗ lồi ra và lõm vào – nên Richardson đã dùng các độ dài bước đi ngày càng nhỏ hơn và mỗi lần làm như vậy lại ghi lại một độ dài L tương ứng. Thay vì vẽ biểu đồ của L so với s, ông có một ý tưởng thông minh hơn là vẽ biểu đồ của log L so với log s (phép toán log ở đây ý chỉ logarit hệ số 10). Dù đường bờ biển trông có vẻ bất quy tắc và ngẫu nhiên, một điều kì diệu đã xảy ra: đồ thị quan hệ này của bờ biển nước Anh và nhiều bờ biển khác trên thế giới dường như là các đường thẳng!

Mỗi đường thẳng đều có phương trình dạng: log L = m log s + b

Sử dụng dữ liệu gốc của Richardson, ta thấy phương trình đường thẳng cho bờ biển ở phía Tây nước Anh xấp xỉ thỏa mãn phương trình:

log L = -0.25 log s + 3.7

Khi ta lấy lũy thừa của cả 2 vế ta được:

L ≈ 5000/(s^0.25)

which when we take the exponent of both sides gives us:

L ≈ 5000/(s^0.25)

Nhưng điều này nghĩa là nếu s càng nhỏ thì L sẽ càng to, và khi s tiến tới 0 thì L sẽ tiến ra vô cùng. Vì các đường bờ biển cũng có thể được xem là các fractal, ta có thể kết luận rằng mọi đường bờ biển thực tế đều dài vô hạn! Điều này nghe hơi sai, khá chắc chắn rằng bạn đã thấy những dữ liệu về độ dài đường bờ biển trước kia, nên tình huống này làm dấy lên câu hỏi:

Chúng ta sai ở đâu?

Tại sao khi thực hiên đo đạc một vật thể hình học, ta lại được kết quả là vô hạn? Hãy lặp lại quá trình này, bằng cách đo chiều dài của một hình vuông. Không chỉ chu vi, cả phần bên trong hình vuông nữa. 

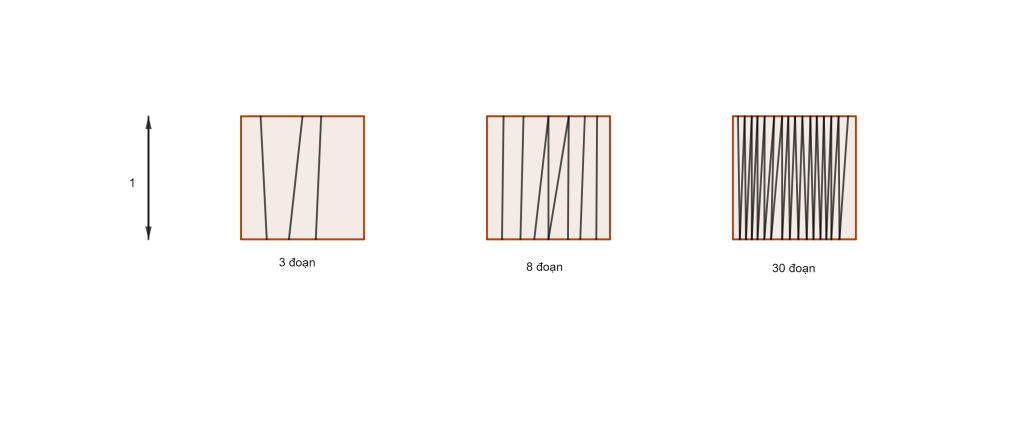
Nhưng ta cần đến bao nhiêu đoạn thẳng mới lấp đầy phần bên trong của một hình vuông? Không quan trọng là bao nhiêu đoạn thẳng, thậm chí là đến khi những đoạn thẳng ở gần nhau tới mức các pixel trên màn hình không thể thể hiện mức độ chi tiết đến thế, vẫn có những chỗ trống trong ô vuông. Ta có thể làm như này mãi mà sẽ luôn có những khoảng trống giữa các đoạn thẳng. Vậy ta có thể kết luận một hình vuông, thì dài vô hạn.

Giờ ta đo thể tích của hình vuông. Rõ ràng nó là 0. Vì hình vuông có chiều dài, chiều rộng, nhưng không có chiều cao. Sau cùng thì, bài học rút ra ở đây là gì?

Ta đang đo bờ biển sai cách. Ở sai chiều không gian.

Một hình vuông thì nên được đo bằng 2 chiều, hay diện tích của nó. Nhưng đường bờ biển là một đường lồi lõm, nên nó không thể có một diện tích. Nhưng nó lại dài vô hạn, nên làm sao nó có thể là một chiều? Có lẽ câu trả lời là cái gì đó ở giữa? Đúng là như vậy. Trước đó, hãy trở lại với những hình Euclid của chúng ta:

Một đoạn thẳng có 1 chiều. Nhân đôi nó lên và kích thước của nó gấp 2^1=2 lần ban đầu

Nhân đôi cạnh của một hình vuông và ta thu được một hình vuông có diện tích gấp 2^2 = 4 lần diện tích ban đầu

Nhân đôi cạnh của một khối lập phương và ta thu được một khối lập phương có thể tích gấp 2^3 = 8 lần thể tích ban đầu

Quy trình này có thể áp dụng được với việc đo đạc đường bờ biển. Ta đã biết rằng chiều không gian của một đoạn thẳng là không đủ để đo đường biên lồi lõm này. Đó là lí do vì sao ta sẽ sử dụng các hình vuông, tận dụng chiều không gian thứ hai của nó.

Tưởng tượng bạn đặt bản đồ nước Anh lên một tấm lưới vuông, và đếm số hình vuông đơn vị mà đường bờ biển đi qua. Giờ dùng một tấm lưới vuông có hình vuông đơn vị có độ dài cạnh nhỏ gấp đôi tấm lưới ban đầu và đếm số hình vuông đơn vị đường bờ biển đi qua một lần nữa. Theo cùng một mạch logic, thì chiều không gian d của bờ biển nên thỏa mãn:
2^d = Số hình vuông đi qua của lưới sau/Số hình vuông đi qua của lưới trước

Nếu ta lặp đi lặp lại thao tác này với những tấm lưới càng ngày càng chi tiết hơn thì giá trị của vế phải sẽ càng ngày càng tiến đến một giá trị nào đó, mà logarit bậc 2 của nó sẽ là giá trị của d. Cụ thể, với bờ biển nước Anh, d xấp xỉ 1.21, một số nằm giữa 1 và 2 đúng như ta dự kiến.