Teaching IFS and applications in Fractal Art using web-based resources (Pt 1)

Materials: Pencil, paper, eraser, tetrahedron pieces, glue, tape, scissors, electronic devices with an internet connection (preferably laptops with Wi-fi)

Goals: Our participants will develop a deep understanding of the iterated function system (IFS) process for generating fractals and will be able to apply it to create various types of natural objects, such as plants, lightning bolts, and snowflakes.

Vocabulary: IFS (iterated function system), fractal, iteration, self-similarity

The Slides:

1. Begin by showcasing captivating images and objects from nature where fractals are observed, emphasizing their prevalence and the idea that fractals serve as the underlying geometry of nature.
2. Introduce a concise yet comprehensive definition of a fractal and illustrate it using an engaging video.
3. Define the IFS concept and provide supporting examples, including classical fractals like the Sierpinski Triangle, Carpet, Tetrahedron, Menger Sponge, Von Koch Curve, and Snowflake. Visual aids and resources from http://blog.sciencevsmagic.net/science/fractal-machine/ can be utilized.

Activities:

1. Craft a Sierpinski Tetrahedron, allowing participants to engage in a hands-on activity that solidifies their understanding of fractals.
2. Facilitate a discussion about the Sierpinski Triangle, asking thought-provoking questions to deepen comprehension. Conclude by highlighting its counterintuitive property: zero area but infinite perimeter.

Theory:

1. Explore the concept of the dimension of self-similar fractals, providing a theoretical framework for understanding their intricate nature.

Quiz:

1. Conduct a quiz to assess participants’ understanding of the concepts covered so far, including questions about the properties of the Koch Curve.

Activities:

1. Engage participants in the process of assembling Sierpinski Tetrahedra, Menger Sponges, or Koch Snowflakes, reinforcing their practical skills in creating fractal structures.
2. Encourage participants to draw natural objects using the IFS technique, allowing them to express their creativity and further explore the connection between art and math. As a fun twist, participants can even draw on macarons, adding a touch of whimsy to their creations.

By combining art and math, this lesson plan aims to inspire participants and ignite their curiosity about the enchanting world of fractals. Through engaging activities and thought-provoking discussions, we hope to foster a deep appreciation for the beauty and complexity of these mathematical wonders.

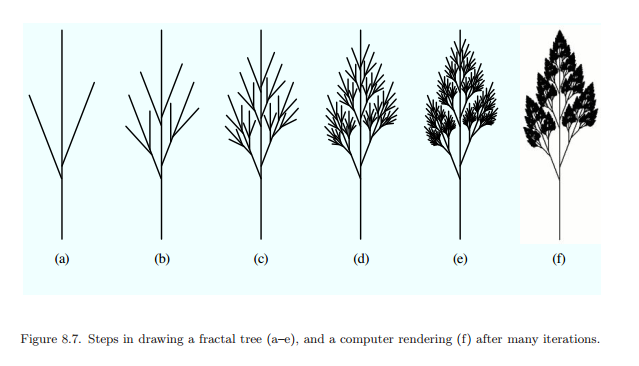
Try drawing something through the lens of fractals. First, use a sharp pencil to draw a tree branch that has no leaves, for example:

 Remember this shape, and replace each of the smaller branching sections with a shrunken version of this initial picture, and you may get something similar to this:

Not that close, but if you have the patience to do this a few times more, then you get 

This is applicable for other types of plants as well, depending on your initial drawing and the details you choose to iterate.

Other subjects that can be drawn this way

Lightning bolt:

Other tree models

Cauliflower

Moon craters