Nút thắt (P3): Thắt chặt sợi dây nối liền nghệ thuật và toán học
Tác giả: Lê Vũ Minh Trí
Sau đây là vài suy nghĩ của mình về tiềm năng khai thác hình ảnh nút thắt trong hai lĩnh vực này.
Với những nút thắt thực tế dùng trong nghệ thuật, ta có thể nối hai đầu dây lại và xem xét cấu trúc đó dưới lăng kính toán học. Tận dụng điều này, ta có thể thử sắp xếp lại thứ tự các phần dây và tạo ra một nút hình thức khác hẳn ban đầu. Ngược lại, với những nút thắt đã biết trong toán học, chuyện chọn ra những cách vẽ 2D đẹp nhất của nút cũng yêu cầu con mắt thẩm mỹ. Chẳng hạn chúng ta xem xét nút ba lá quen thuộc sẽ biến hóa ra sao với đường nét và cách xếp nút khác nhau:

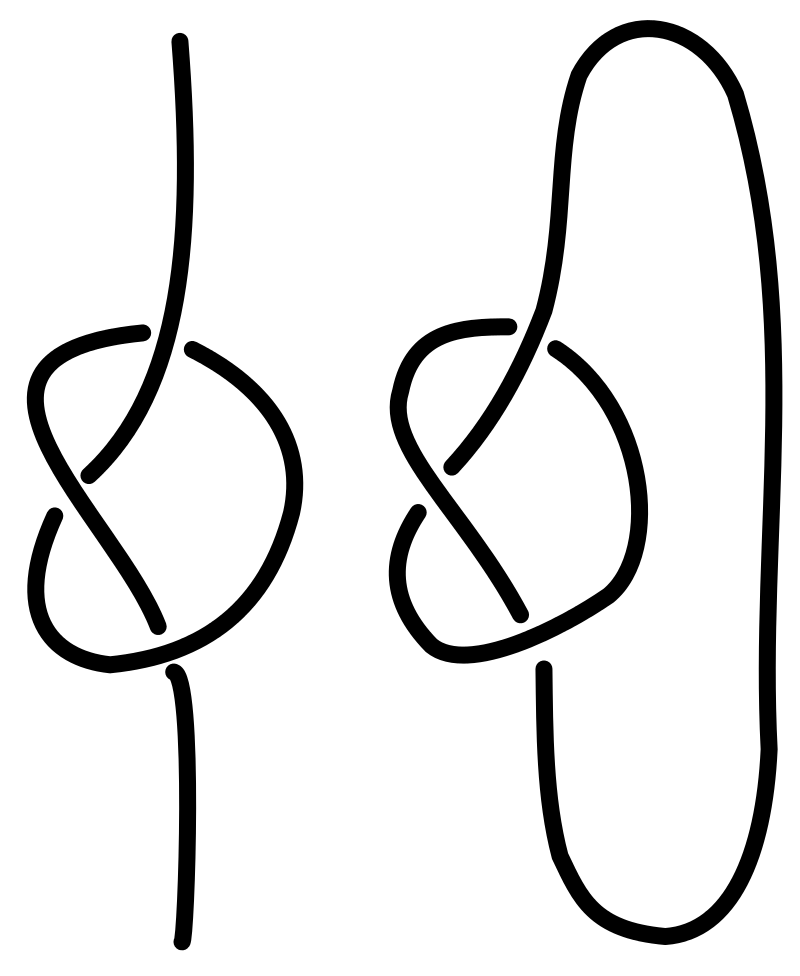





Và đây mới chỉ là nút không tầm thường đơn giản nhất. Lấy ví dụ với macrame
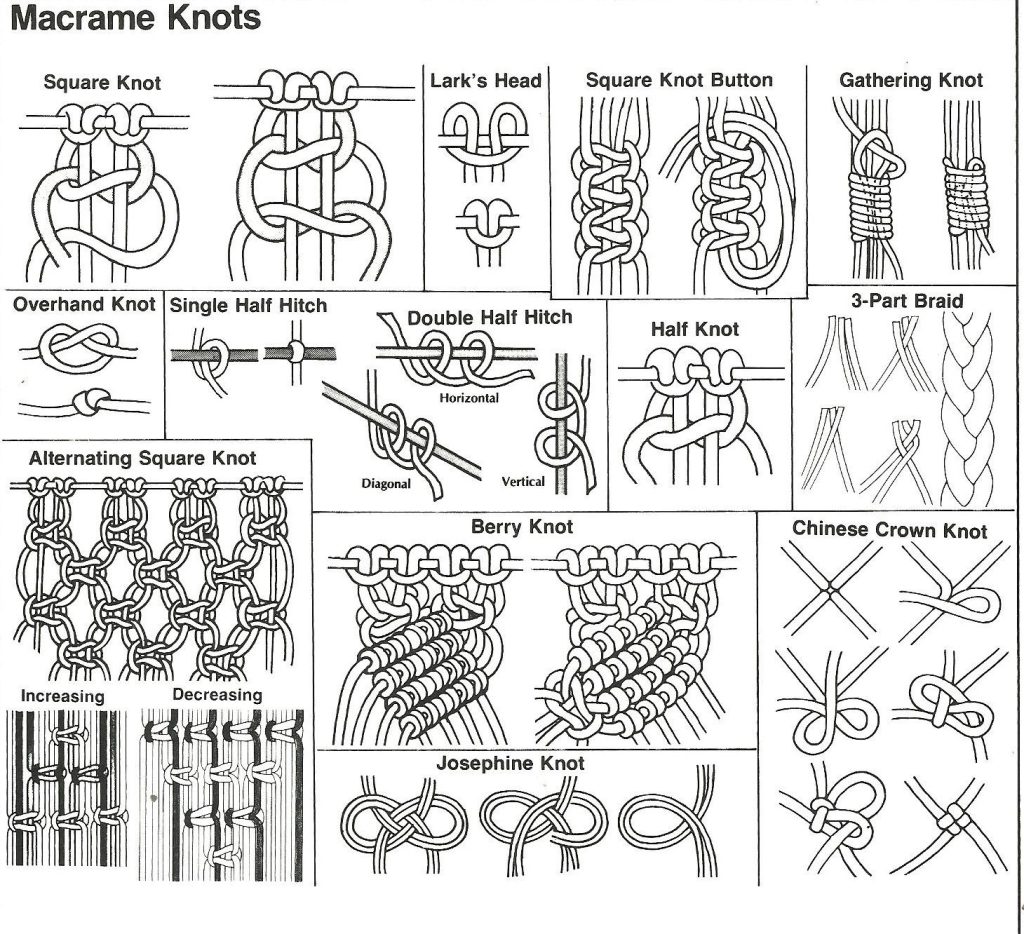
Trông thì có vẻ hơi nhiều, nhưng thực chất chỉ cần 3-4 loại là đã có thể tạo nên một tác phẩm macrame hoàn chỉnh: lark’s head knot hầu như để cố định dây vào khung, square knot và hai loại half hitch knot dùng làm họa tiết. Thậm chí cột bên trái của hình ảnh này là dành cho các cách tạo họa tiết square knot.
Một trong những mục đích của WMMA là tìm cách truyền tải lại nội dung các kiến thức liên quan đến cả hai lĩnh vực sao cho dễ hiểu nhất. Hiện tại chưa có bài giảng, và mình sẽ chỉ nêu sơ qua vài ý tưởng để hoàn thiện trong tương lai.
Bài giảng nên cho phép các bạn sử dụng dây thoải mái để thắt và hiểu hơn các nút. Các hình minh họa về mặt nghệ thuật có thể tham khảo bài viết đầu tiên, khi cho các bạn thử tự vẽ thì có thể thử nút Celtic. Nội dung bài giảng theo mình có thể đi theo bài viết phần 2, gồm:
- Cách vẽ và cách gỡ nút (theo nghĩa toán học)
- Làm sao để chứng tỏ hai nút là khác nhau: bất biến tô màu và bất biến đa thức
- Link và Braid
Tùy thuộc vào học sinh có thể thêm bớt nội dung. Chẳng hạn với các bạn nhỏ tuổi hơn nên nói kỹ hơn về cách vẽ nút trong toán học và dành thêm thời gian và bài tập để đảm bảo các bạn hiểu (ví dụ như bảo các bạn nối các nút trên bảng bằng dây được phát sẵn). Phần đa thức thì các nguồn khác thường giới thiệu đa thức một biến Alexander-Conway, thật ra mình cảm thấy ví dụ bằng HOMFLY với các nút đơn giản sẽ không khó hơn quá, nhưng nhìn chung nội dung này nên dành cho các bạn lớn chút, cấp 3 trở lên chẳng hạn. Các bài tập sẽ xoay quanh các vấn đề cơ bản đã đặt ra (phân biệt hai nút, biến đổi giữa các biểu diễn, gỡ nút, tập sử dụng các bất biến cơ bản), trong đó cố gắng tăng dần độ khó tới mức không hiển nhiên kể cả với các bạn cấp 3 (có thể kể đến sơ đồ Ochiai là một unknot (không nút) không dễ thấy). Một vài câu hỏi nhỏ về mặt lý thuyết khác có thể kể đến như: có nút nào 1 hay 2 điểm giao không, hay tại sao bảng của Tait lại bắt đầu từ nút 3 điểm giao trở đi?
Mình có nghĩ đến một hoạt động nhận diện nút như sau: mỗi đội khoảng 2-3 người được bí mật đưa cho một nút thuộc vào một trong số các nút cho trước trên bảng (chẳng hạn như các nút nguyên tố không có quá 7 điểm giao trong bảng của Tait). Mỗi đội sẽ có một khoảng thời gian để thắt và làm rối nút được cho tùy ý, miễn sao vẫn gỡ trở lại nút ban đầu được. Sau đó các thành viên sẽ phân chia nhau thành các nhóm (có thể ghép giữa các thành viên của đội khác nhau) đi gỡ nút của các đội khác, mỗi nhóm mới có đúng một cơ hội để gọi tên nút mình đang gỡ. Chỉ cần gọi tên đúng, không cần gỡ hết. Ai nêu được nút đúng càng sớm sẽ đạt được điểm càng cao cho đội của mình. Nút nào bị phát hiện càng muộn càng cộng nhiều điểm cho đội đó.
Để kết lại, loạt bài viết này có thể không tươi sáng lắm, nhưng có thể knot theory vẫn đang chờ ai đó như Escher với tessellation, Robert Lang với origami, hay Mandelbrot với fractal. Điều quan trọng không ngừng tìm tòi và thử nghiệm các ý tưởng. Biết đâu ai đó đọc bài viết này sẽ có ý tưởng nào đó thì sao?
