Nút thắt (P2): Góc nhìn từ Toán học
Tác giả: Lê Vũ Minh Trí

Phân môn nghiên cứu về các nút trong toán học được gọi là lý thuyết nút thắt, một phần của tô pô. Một nút thắt trong toán học về cơ bản giống như một sợi dây uốn lượn thoải mái, sau đó hai đầu dây được nối lại. Khác với những sợi dây thực thế, ta có thể bóp méo và chuyển vị trí các nhánh của nút tùy thích, miễn sao nút không bị rách. Đây cũng là tinh thần chung của tô pô, nơi ta hầu như có thể bóp nắn các chi tiết như đất nặn, và bánh donut với cái cốc là một:
Năm 1771, Vandermonde lần đầu phát triển một lý thuyết toán học cho các nút thắt và lưu ý đặc tính tô pô của các nút. Sang thế kỷ sau, có những đóng góp như tích phân đếm số lần hai nút cắt nhau của Gauss, nhưng nổi bật nhất phải kể đến giả thuyết của Nam tước Kelvin (thang nhiệt độ Kelvin đặt theo tên ông). Khi xem máy tạo khói của Peter Guthrie Tait phụt ra những vòng hóa chất hoàn hảo, ông đã đề ra một giả thuyết về hình dáng của các nguyên tử: chúng chính là các loại nút khác nhau cấu tạo từ aether (ê te), một vật chất vô hình tồn tại khắp nơi. Tait có chút hoài nghi, song bị thuyết phục bởi lý thuyết dần nổi tiếng của Kelvin, đã bắt tay vào lập bảng tất cả các nút theo số giao điểm. Về sau các nhà khoa học phát hiện ra qua thực nghiệm là aether không tồn tại, và dù thuyết của ngài nam tước đi vào dĩ vãng, đây lại là khởi đầu cho một ngành lý thuyết còn nhiều câu hỏi bỏ ngỏ và tiềm năng phát triển trong tương lai.
Có hai câu hỏi gắn với các nút: nút thắt trong toán học có hình dáng trông thế nào, và làm thế nào để gỡ các nút?
Cách vẽ và gỡ một nút
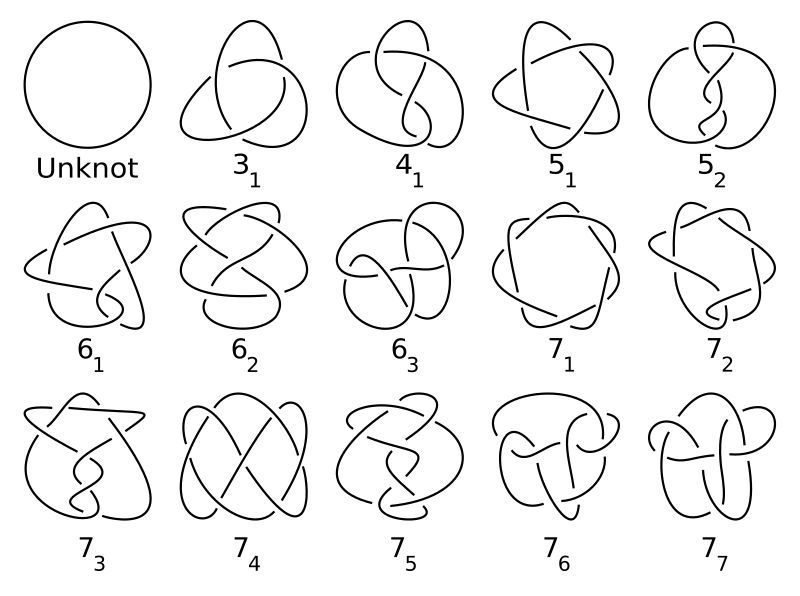
Câu hỏi đầu tiên dễ trả lời hơn, trong toán học có cách vẽ nút cũng khá dễ hiểu, chẳng hạn như nhìn hình dưới đây. Hình bên chính là một phần trích ra từ bảng nút của Tait.
Ở các phần hai dây cắt nhau, ta thấy có dây đứt đoạn ở nơi đáng ra là giao điểm. Vẽ như vậy là để ám chỉ sợi đứt chính là sợi nằm ở dưới.
Còn câu hỏi “làm thế nào để gỡ các nút” thì thực tế có nhiều cách. Cách đơn giản nhất là tái tạo cái nút bằng một đoạn dây và thử mần mò thôi, mỗi người sẽ có một cách tiếp cận chuyện gỡ nút. Tuy nhiên, các nhà toán học thường muốn có cách để áp dụng một lời giải cho vô hạn nút và ta không thể nói rằng “tôi đã thắt cái nút đó trong thực tế và khi kéo căng ra nó về một vòng tròn” với tất cả các nút được.
Người ta đã chỉ ra được để gỡ nút ta chỉ cần tói ba thao tác cơ bản sau, gọi là thao tác Reidemeister:
1. Duỗi thẳng một đoạn dây bị xoắn tại một điểm nhỏ
2. Trượt hai phần dây không bị cuốn với nhau ra xa
3. Cho một sợi nằm trên/ dưới trượt qua một điểm giao
Mô tả sẽ khó hơn nhìn hình vẽ nên đây là hình vẽ ba thao tác này.
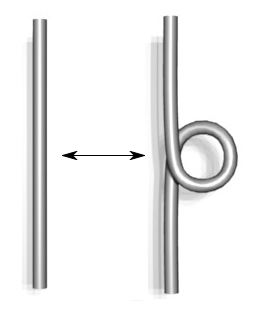
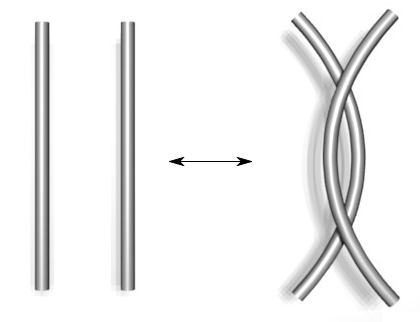
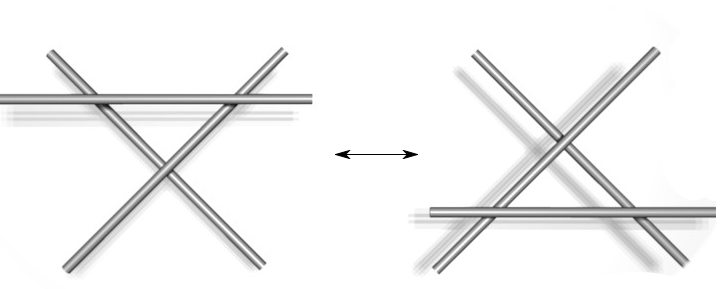
Một câu hỏi hợp lý khác, vẫn liên quan đến hai thắc mắc trên, là tồn tại bao nhiêu nút, làm thế nào để đếm được hết các nút và đảm bảo mình không đếm trùng hai nút nào đó? Chẳng hạn, chúng ta thấy vòng tròn được gọi là unknot hay không-nút kia chẳng có giao điểm nào, nhưng liệu nút ba lá (trefoil) có thật là một nút khác với không-nút không? Ta có thể thử gỡ nút ba lá, và dù cố cỡ nào cũng không biến đổi về không-nút được. Nhưng mình không làm được đâu có nghĩa là không có cách, ta phải chứng minh là không thể làm được mới xong. Ngược lại, có những hình vẽ biểu diễn cùng một nút nhưng chưa chắc ta dễ dàng phát hiện. Bảng nút của Tait cũng chẳng phải ngoại lệ, nhưng lỗi sai đó phải đợi ngót nghét cả thế kỷ mới bị phát hiện bởi Kenneth Perko vào năm 1973. Nếu bạn cảm thấy chuyện hai nút này là hiển nhiên, nên nhớ rằng cặp nút này có số thứ tự là 161 và 162 trong bảng nút ban đầu đó!
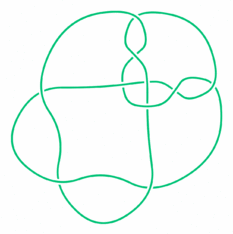
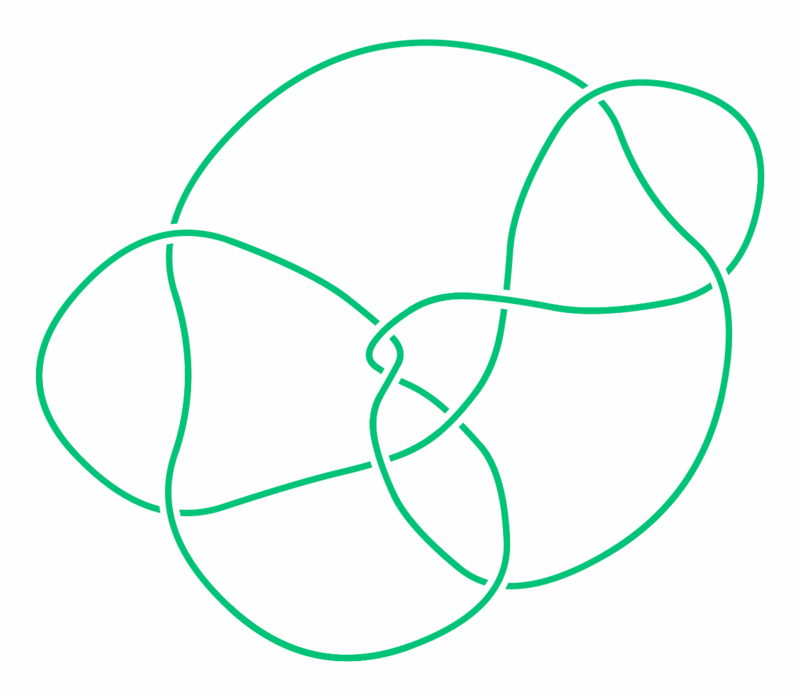
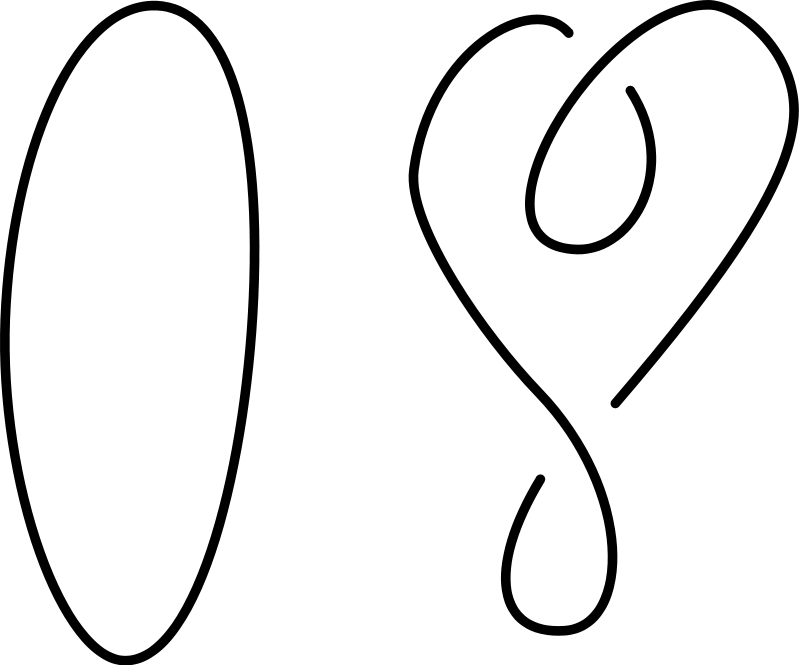
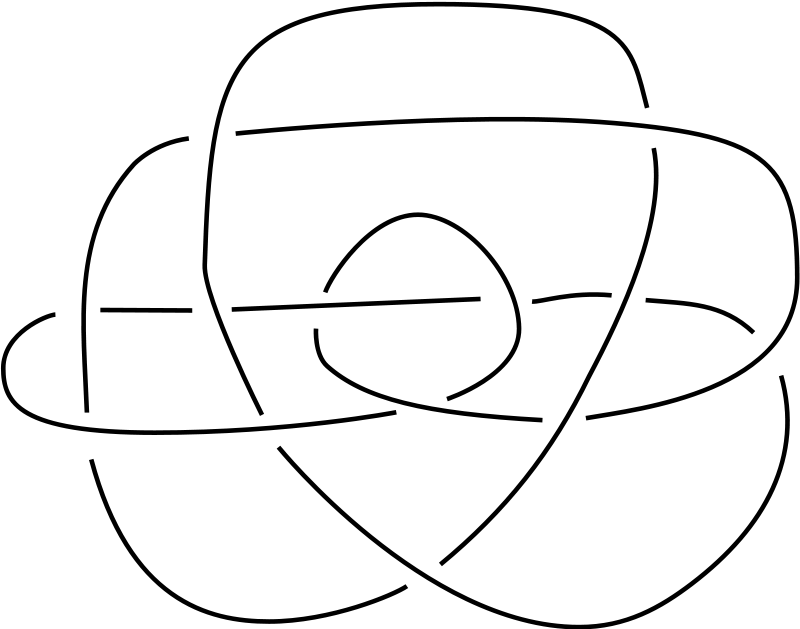
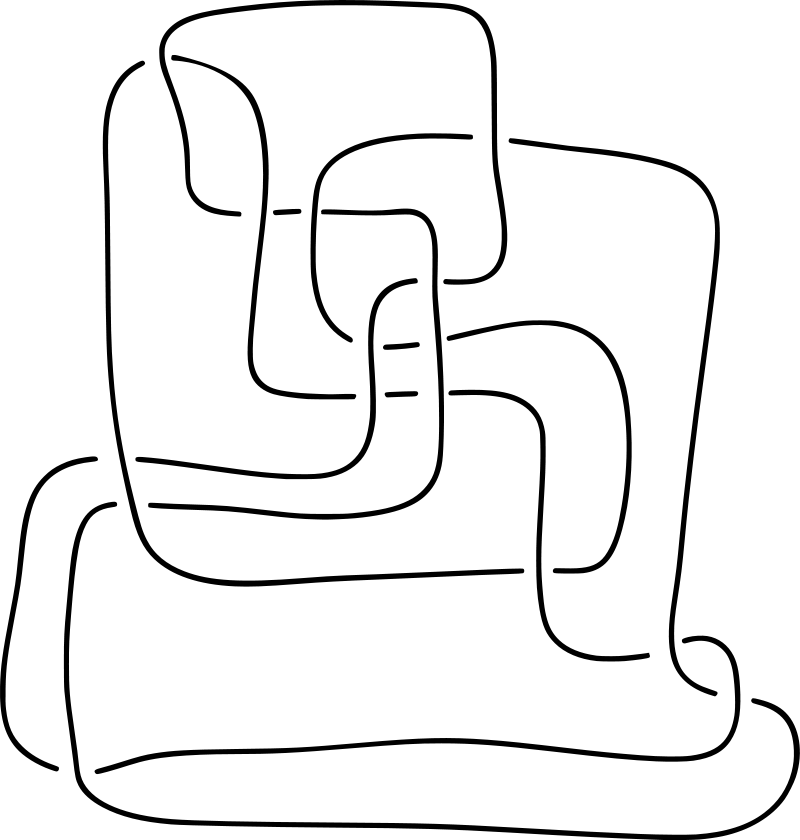

Trong những nút này có bao nhiêu loại nút phân biệt?
Vậy làm thế nào để phân biệt hai nút và chứng tỏ hai nút phân biệt, từ đó làm sao để tìm được các nút mới? Bài toán này, bài toán nhận diện nút, là một bài toán căn bản còn đang để ngỏ, và chúng ta hãy cùng điểm qua vài cách để tấn công nó.
Bất biến
Giải pháp là các bất biến, tức là một tính chất gì đó của nút không đổi khi ta gỡ nó. Tính chất đó có thể là gì? Sự uốn lượn của nút? Không phải, vì ta có thể bẻ thẳng và uốn cong sợi dây thoải mái. Số điểm giao? Chưa hẳn, vì mình có thể xoắn nút lại mãi và mỗi lần xoắn sẽ thêm một điểm giao.
Ta có một bất biến từ việc trang trí nút thắt gọi là tricolorability, tức là liệu nút thắt có tô được bằng ba màu không. Cụ thể, ta xét xem một nút có thể tô được bởi ít nhất hai màu sao cho tại mỗi giao điểm thì 3 nhánh dây (nhánh trên và hai nhánh dưới) hoặc là cùng một màu, hoặc là đôi một khác màu. Để chỉ ra đây thật sự “bất biến”, ta chỉ cần kiểm tra nó có thay đổi qua các thao tác Reidemeister không. Đây chính là một tình huống tỏ rõ sự hữu dụng của các thao tác Reidemeister.
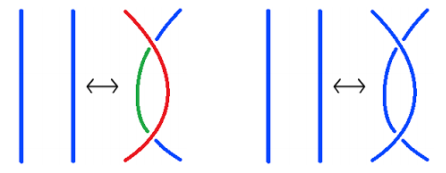
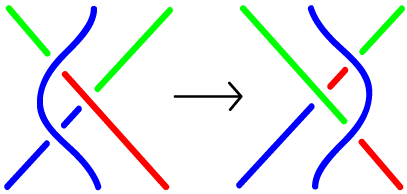
Qua hình ta thấy là không: nút tô ba màu được vẫn cứ tô ba màu được khi gỡ và ta hoàn tất.
Ngay lập tức ta phân biệt được nút ba lá với nút không, và thậm chí là nút ba lá với nút số 8, do nút ba lá tô ba màu được, còn hai nút kia thì không.
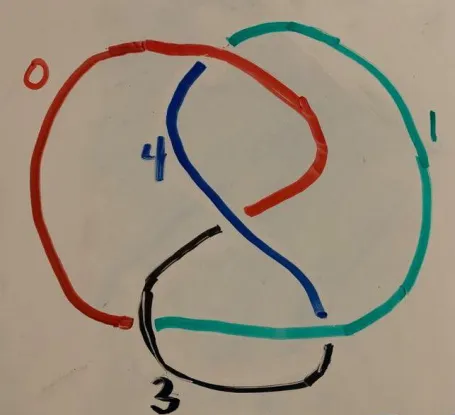
Tổng quát hơn tricolorability là p-colorability, trong đó ta đánh số p màu từ 1 đến p, sao cho mỗi nhánh có một số, có ít nhất hai số được dùng, và tại mỗi điểm giao thì hai lần số ở nhánh trên trừ đi hai số nhánh dưới chia hết cho p.
Qua hình vẽ này ta thấy nút số 8 tô màu 5 được còn nút ba lá và nút không thì không.
Hạn chế của bất biến này là nó chỉ chia nút ra làm hai loại: hoặc là tô được hoặc không tô được. Vì thế các nhà toán học tìm kiếm các phương cách khác: họ không chỉ dùng số mà dùng hẳn đa thức để gắn cho các nút. Đôi khi đây là một quá trình thử nghiệm, trong đó các nhà toán học dựa vào các quan sát và kiểm tra lại tính bất biến bằng thao tác Reidemeister để tạo nên một bất biến đa thức. Thậm chí có trường hợp kỳ khôi của Vaughan Jones đạt giải Fields nhờ tình cờ phát hiện ra một đa thức giống các đa thức nút từ trước trong lúc nghiên cứu một lĩnh vực gần với vật lý hơn. Nhận thấy đa thức này nhạy hơn các bất biến trước đó, cộng đồng nhanh chóng tiếp thu và nâng cấp bất biến của Jones, cho ra đời đa thức HOMFLYPT. Đa thức này thậm chí có hai biến l, m, hình thành theo quy tắc sau:
với các điểm giao được đặt tên như sau
Thế nhưng hiện vẫn chưa biết bất biến tối thượng nào để phân biệt hai nút bất kỳ với nhau.
Ghép nút, lồng nút, cắt nút
Ta có thể nghịch nút nhiều hơn là chỉ ngắm và nhận diện chúng.
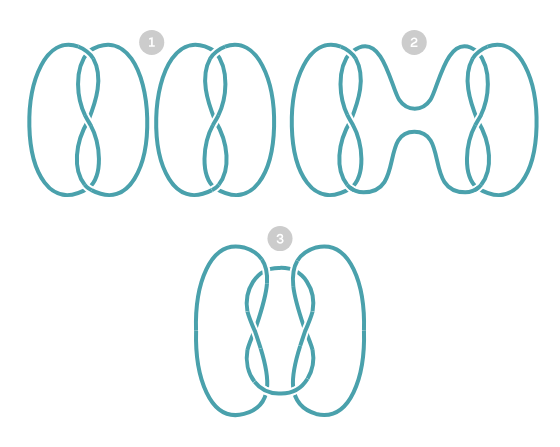
Làm thế nào để ghép các nút với nhau thành một nút lớn? Thao tác này gọi là cộng nút, được thực hiện giống như hình vẽ bên cạnh. Đây là nút vuông, bằng tổng hai nút ba lá, và là một trong những nút phổ biến nhất của macrame.
Hơi khác với tổng thông thường, có thể có tối đa 2 cách cộng hai nút với nhau, chẳng hạn như khi ta cộng nút gọi là 817 với chính nó.
Để giải quyết chuyện này, người ta sẽ định hướng các nút để tổng có được là duy nhất.
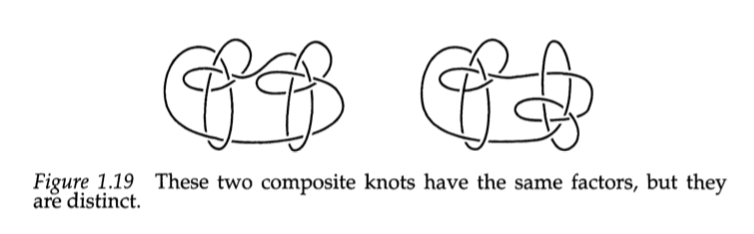
Tương tự với số tự nhiên, ta có khái niệm nút nguyên tố. Giống số nguyên tố trong số tự nhiên là số không thể viết thành tích hai số tự nhiên không tầm thường (1 là tầm thường vì số nào cũng tách 1 ra được), nút nguyên tố là nút không phải tổng của hai nút tầm thường (tức là khác không-nút) nào. Và may cho chúng ta, lại có một kết quả về các nút là với phép cộng có hướng thì mỗi nút khác không-nút có đúng một cách tách ra thành tổng các nút nguyên tố. Lờ mờ cảm nhận được điều đó, Tait chỉ liệt kê các nút nguyên tố trong bảng của mình.
Các nút có thể lồng với nhau được, chẳng hạn như hai không-nút lồng với nhau, biểu tượng Thế vận hội Olympic, hay là vòng Borromeo mà chỉ cần bỏ một vòng là gỡ được hai vòng còn lại. Các nút được lồng với nhau này được gọi chung là link.




Từ đầu chúng ta đã nói về chuyện không được cắt nút ra như Alexander Đại đế. Thật ra vẫn có cách để vượt qua rào cản này, và nó cho ta một cách biểu diễn nút khác. Cuộn nút tùy ý, rồi chọn ra một đoạn dây không có điểm giao nào, cắt dây ở đó, rồi dán mỗi đầu vào một thanh ngang. Ta được một braid, trông giống như hình bên.
Định lý Alexander (và thật ra ta cũng tự cảm thấy điều này phải đúng) khẳng định rằng mọi nút hay link đều cắt thành braid được. Mỗi braid khi chập hai đầu lại chỉ cho ra một nút, nhưng cũng có nhiều cách cắt nút cho ra các braid khác nhau. Braid cho phép ta tách riêng (dịch lên xuống) từng đoạn các dây cắt qua nhau để quan sát cấu trúc nút kỹ hơn và thấy lần lượt các thao tác chuyển dây tạo thành nút. Nó cho ta cả một các cộng nút khác: chập thanh ngang dưới của nút này với thanh ngang trên của nút kia rồi nối các dây ở cột tương ứng với nhau thôi.
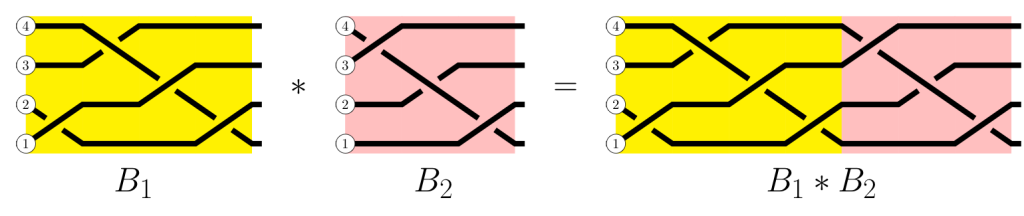
Các braid có nhiều điểm giống với macrame, nhưng nếu xét nhóm Artin của các braid trong toán học, thao tác vắt dây để thắt nút vuông trong macrame là không hợp lệ. Tất nhiên người ta thay đổi chút để thành hợp lệ được.
Gợi mở những ứng dụng
Công dụng của những nút thắt từ xưa có gì nay vẫn có đấy là chuyện thường, nhưng dần người ta cũng khám phá ra nhiều ứng dụng và nơi khác xuất hiện các nút. Lý thuyết nút thắt có thể được dùng để nghiên cứu cấu trúc siêu xoắn của ADN trong nhiều tình huống, và hiện có một hướng nghiên cứu phát triển máy tính lượng tử gọi là tô pô lượng tử, với ý tưởng làm các qbit ổn định hơn trước các biến động ngoại lai khi ta cho chùng bất biến về mặt tô pô thay vì mặt hình học thông thường.
Qua hai bài viết kể trên, mọi người có thể lờ mờ đoán ra tại sao lại có sự phân chia này.
Bởi theo mình nhìn nhận, hình thức của các nút phổ biến trong nghệ thuật và toán học, cũng như mối quan tâm của nghệ sĩ và các nhà toán học có nhiều khác biệt, thậm chí là khác xa. Thế nhưng nút thắt vẫn là một cầu nối giữa cả hai lĩnh vực lại, nhờ một giá trị hết sức đơn giản: vẻ đẹp của chúng. Chỉ là, hình thức của những nút được quan tâm trong nghệ thuật và toán học khác biệt do mục đích của hai bên thôi. Các nhà toán học nối hai đầu dây quấn nút lại và tìm kiếm thật nhiều loại nút khác nhau, trong khi các nghệ sĩ tìm cách vận dụng khéo léo một số ít những chi tiết đơn giản và sáng tạo ra các tác phẩm thắt nút mới mẻ.
